COMPLEXES (NOMBRES)

COMPLEXES (NOMBRES)

Introduits à l’origine comme symboles purement formels destinés à rendre compte des propriétés des équations algébriques, les nombres imaginaires sont d’un usage courant au XVIII^e siècle, mais ce n’est qu’au siècle suivant qu’ils seront définis et utilisés correctement, avec la rigueur qui caractérise les préoccupations des mathématiciens du XIX^e siècle. Et c’est alors le prodigieux essor de la théorie des fonctions d’une variable complexe et l’entrée en force des imaginaires dans presque tous les domaines des mathématiques. De nos jours, les nombres complexes interviennent de manière essentielle, comme un cadre naturel, dans maintes théories mathématiques et physiques.

1. Historique

Les nombres «impossibles»

Alors que de nombreux mathématiciens (dont Viète) hésitaient encore à utiliser les nombres négatifs, les algébristes italiens du XVI^e siècle, Cardan et ses élèves, s’enhardirent à introduire dans les calculs des symboles purement formels 連漣 a , a 礪 0, représentant le résultat de l’extraction «impossible» de la racine carrée du nombre négatif 漣 a ; ils décrivent en détail des règles de calcul permettant de manipuler ces nouveaux «nombres», appelés par eux nombres impossibles.

À l’origine, il s’agissait seulement de donner des racines à toutes les équations du second degré; les résultats obtenus dans l’étude de l’équation du troisième degré allaient familiariser les mathématiciens avec ces symboles et mettre en évidence leur rôle comme intermédiaire commode de calcul dans de nombreux cas. Au moyen de la formule dite de Cardan ^{[cf. ÉQUATIONS ALGÉBRIQUES]}, Bombelli montre, en 1572, que la racine x = 4 de l’équation x ³ = 15 x + 4 peut s’écrire:

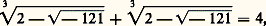mettant par là en évidence le fait que certaines quantités réelles peuvent être représentées par des expressions en apparence imaginaires. Ainsi, la formule de Cardan permet de représenter des racines réelles par l’intermédiaire d’opérations effectuées sur des nombres impossibles, ou «imaginaires». Les nombres imaginaires fournissent donc des méthodes de calcul, de nature certes mystérieuse, mais qui permettent d’obtenir des résultats «vrais» qu’il serait souvent beaucoup plus long ou beaucoup plus difficile d’obtenir directement.

Pour ces raisons, somme toute empiriques, les mathématiciens utilisèrent avec une confiance croissante les nombres imaginaires depuis le début du XVII^e siècle. Dès 1629, A. Girard soupçonnait que toute équation de degré n a n racines réelles ou imaginaires, ce qui revenait à pressentir que les nombres imaginaires constituent le cadre «naturel» de la théorie des équations. À partir de 1675, Leibniz applique avec succès ses méthodes (de développements en série par exemple) aux nombres imaginaires et obtient ainsi de nombreux résultats, tandis qu’A. de Moivre, au début du XVIII^e siècle, met en évidence, par une utilisation systématique de la trigonométrie, les liens entre la recherche des racines des nombres imaginaires et la division d’un arc de circonférence en parties égales.

La possibilité, admise implicitement, d’étendre aux nombres complexes la plupart des notions relatives aux nombres réels allait se trouver mise en question par la controverse des logarithmes des nombres complexes, dont l’intérêt était apparu, par analogie avec le cas des pôles réels, dans l’intégration des fractions rationnelles. Les différentes formules contradictoires obtenues suscitèrent contre les imaginaires un vent de méfiance, qui fut dissipé par L. Euler; celui-ci comprit qu’il fallait abandonner le caractère univoque du logarithme pour obtenir une théorie satisfaisante et établit d’innombrables formules relatives aux fonctions élémentaires d’une variable complexe ^{[cf. EXPONENTIELLE ET LOGARITHME]}.

À la fin du XVIII^e siècle, les imaginaires sont d’usage courant, mais leur «existence mathématique» véritable n’est pas établie; c’est aux mathématiciens du XIX^e siècle qu’il appartenait de les construire à partir des quantités connues, de leur donner une «réalité mathématique». Avec Cauchy, c’est le prodigieux essor de la théorie des fonctions d’une variable complexe et le début de l’analyse contemporaine (cf. ANALYSE MATHÉMATIQUE et FONCTIONS ANALY- TIQUES).

Théorie géométrique

L’idée, non seulement de représenter les nombres imaginaires par les points du plan, exprimée maladroitement par Wallis dès 1685, mais de les définir à partir de ces notions, est apparue dans deux mémoires, passés inaperçus à l’époque, du Danois Wessel (1798) et du Suisse Argand (1806). En fait, c’est Cauchy qui diffusera ce point de vue.

Dans le plan muni de deux axes de coordonnées Ox et Oy , on dira que les vecteurs d’origine O portés par Ox définissent les nombres réels, tandis que les autres vecteurs d’origine O définissent les nombres imaginaires; le terme nombres complexes recouvre à la fois les nombres réels et les nombres imaginaires.

L’addition des nombres complexes se définit à partir de l’addition usuelle des vecteurs. Pour la multiplication, on fait la construction suivante: soit OUle vecteur unitaire de l’axe Ox ; le vecteur OC«produit» des vecteurs OAet OBs’obtient alors en construisant sur OAun triangle OAC directement semblable au triangle OUB (fig. 1). À partir de là, on retrouve géométriquement toutes les propriétés des nombres complexes.

Le nombre complexe i est défini par le vecteur unitaire de l’axe Oy , et la multiplication d’un vecteur OApar i revient donc à prendre un vecteur OAdirectement perpendiculaire à OA 轢; répétant cette opération, on obtient le vecteur OAopposé du vecteur OA 轢, c’est-à-dire que la multiplication par i ² revient à multiplier par le nombre réel 漣 1.

Théorie arithmétique

La théorie géométrique présente l’inconvénient de subordonner toutes les propriétés algébriques des nombres complexes à des considérations géométriques qui peuvent sembler étrangères. La théorie arithmétique, due à Hamilton (1835), consiste à considérer les nombres complexes comme des couples de nombres réels et à définir la somme et le produit par des formules explicites; nous n’insisterons pas davantage ici sur cette approche, que nous exposerons ci-dessous. Ce point de vue conduit à essayer de définir plus généralement des opérations d’addition et de multiplication pour des systèmes de n nombres réels et a conduit Hamilton à introduire les quaternions et plus généralement les algèbres de dimension finie (appelées, au XIX^e siècle, systèmes hypercomplexes ; cf. ANNEAUX ET ALGÈBRES).

Les équivalences algébriques

Dès 1847, Cauchy considère que les calculs sur les nombres complexes reviennent à calculer sur les polynômes en la variable i , soumis aux règles usuelles de l’algèbre, en remplaçant i ² + 1 par 0; cela revient à considérer que deux polynômes sont équivalents, c’est-à-dire définissent le même nombre complexe, si leur différence est divisible par i ² + 1. Dans le langage contemporain, cela revient à définir l’ensemble des nombres complexes comme des classes d’équivalence de polynômes à coefficients réels modulo le polynôme irréductible X² + 1. C’est cette approche qui allait conduire Kronecker à la théorie générale des corps de nombres algébriques (cf. CORPS [mathématiques]).

2. Le corps des nombres complexes

Construction

Par définition, un nombre complexe sera un couple z = (x , y ) de deux nombres réels; si z = (x , y ) et z = (x , y ) sont deux nombres complexes, on appelle alors somme et produit de ces deux nombres complexes les nombres complexes:

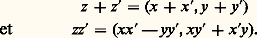Il est alors facile de vérifier que, pour ces deux opérations, l’ensemble des couples de nombres réels est un corps, le corps C des nombres complexes ; par exemple, si z = (x , y ) (0, 0), son inverse est le nombre complexe:

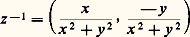aussi noté 1/z .

Il est aussi souvent commode de représenter géométriquement le nombre complexe z = (x , y ) par le point M de coordonnées (x , y ) dans le plan muni d’un système d’axes de coordonnées orthonormé; M s’appelle l’image de z et il est clair que tout point M du plan est l’image d’un unique nombre complexe appelé affixe de M.

Les nombres complexes de la forme (x , 0) forment un sous-corps de C qui est isomorphe au corps R des nombres réels par l’application qui à (x , 0) fait correspondre x ; dans la suite, nous identifierons donc le nombre complexe (x , 0) au nombre réel x , ce qui fait apparaître R comme un sous-corps de C. Parmi les nombres complexes, les nombres réels ont donc pour images les points de l’axe Ox , appelé pour cette raison axe réel ; remarquons que si a est un nombre réel, le produit de a et du nombre complexe z = (x , y ) est simplement az = (ax , ay ).

Le nombre complexe i = (0,1) vérifie i ² = 漣 1, et tout nombre complexe z = (x + y ) peut s’écrire de manière unique z = x + iy , pour x et y réels; nous adoptons désormais cette écriture, dite cartésienne, pour tout nombre complexe. Les nombres réels x et y s’appellent respectivement la partie réelle et la partie imaginaire de z et on note:

Les nombres complexes écrits sous forme cartésienne satisfont aux règles usuelles du calcul élémentaire, en tenant compte du fait que i ² = 漣 1; par exemple:

ce qui redonne la formule ci-dessus du produit. Les nombres complexes non nuls de la forme iy , y 捻 R, ont pour carré le nombre réel négatif 漣 y ²; pour cette raison, ils sont dits imaginaires purs et l’axe Oy est appelé l’axe imaginaire .

On appelle conjugué du nombre complexe z = x + iy le nombre complexe 磻 = x – iy ; l’application de conjugaison, qui à tout nombre complexe fait correspondre son conjugué, est un automorphisme involutif du corps C, c’est-à-dire que l’on a:

il en résulte par exemple que si z 0, alors 磻 0 et 1/z = 1/ 磻 .

Pour tout nombre complexe z , le produit N (z ) = zz = x ² + y ² est un nombre réel positif; c’est le carré de la distance de l’image de z à l’origine des coordonnées. On appelle module de z le nombre réel positif: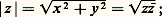

le module des nombres complexes possède les mêmes propriétés que la valeur absolue des nombres réels: |z | = 0 si et seulement si z = 0;

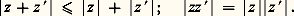Remarquons que l’inverse d’un nombre complexe non nul est égal à 1/z = z /|z |²; en particulier, les nombres complexes de module 1, sur lesquels nous reviendrons, ont pour inverse leur conjugué.

Le théorème fondamental de l’algèbre

Les nombres complexes sont donc apparus très tôt comme le domaine naturel de la théorie des équations algébriques: toute équation algébrique peut être résolue dans ce corps. Plus précisément, le résultat fondamental est le suivant. Si P est un polynôme de degré n à coefficients complexes, il existe n nombres complexes a ¹, a ², ..., a ⁿ , pas nécessairement distincts, tels que l’on ait identiquement:

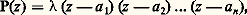où est le coefficient du terme de plus haut degré. Ainsi, si l’on appelle ordre de multiplicité d’une racine le nombre de fois où elle apparaît dans la décomposition ci-dessus, tout polynôme de degré n a exactement n racines, chacune étant comptée avec son ordre de multiplicité.

Cette propriété était implicite pour de nombreux mathématiciens, mais c’est à d’Alembert que l’on doit la première tentative de démonstration, d’où le nom de théorème de d’Alembert que l’on donne souvent à cet énoncé. La démonstration de d’Alembert (1746) repose sur une argumentation analytique habile mais qui utilise des résultats de topologie. On doit à Euler (Recherches sur les racines imaginaires des équations , 1751) la première tentative de démonstration algébrique, qui fut reprise et améliorée tout au cours du XVIII^e siècle par Lagrange, Laplace et d’autres. Mais ces démonstrations présentaient toutes des lacunes importantes. Gauss, dans sa dissertation de 1799, en fait l’historique critique et donne la première démonstration complète. Il reviendra à plusieurs reprises sur ce sujet et ne donnera pas moins de quatre démonstrations différentes du théorème fondamental de l’algèbre. Les développements de la théorie des fonctions de variable complexe au XIX^e siècle ont vu naître d’innombrables démonstrations de ce résultat (cf. FONCTIONS ANALYTIQUES - Fonctions analytiques d’une variable complexe, chap. 4).

Un corps sur lequel tout polynôme se décompose en facteurs du premier degré est dit algébriquement clos (cf. CORPS [mathématiques]); cette propriété explique par exemple pourquoi la théorie des courbes algébriques se développe plus harmonieusement sur le corps des nombres complexes que sur le corps des nombres réels ^{[cf. COURBES ALGÉBRIQUES]}.

Limites

Puisque le module des nombres complexes possède les mêmes propriétés que la valeur absolue des nombres réels, on peut définir de manière analogue toutes les notions relatives aux limites; remarquons d’ailleurs que les définitions qui suivent, appliquées au cas particulier des nombres réels, redonnent toutes les notions correspondantes pour ces nombres.

On appelle suite de nombres complexes la donnée, pour tout entier naturel n , d’un nombre complexe z ⁿ ; la suite correspondante est alors notée (z ⁿ ). On dit qu’une suite (z ⁿ ) de nombres complexes tend vers une limite u , ou converge vers u , pour n tendant vers l’infini, si pour tout nombre 﨎 strictement positif, on a:

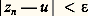pour n assez grand, c’est-à-dire sauf pour au plus un nombre fini d’entiers n. On écrit alors:

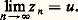La limite si elle existe est déterminée de manière unique, et toutes les propriétés usuelles des suites de nombres réels ne faisant pas intervenir la relation 諒 sont valables ici; en particulier, le critère de Cauchy, qui permet d’affirmer qu’une suite est convergente sans connaître sa limite, s’applique.

Les séries de nombres complexes jouent un rôle absolument essentiel car elles interviennent dans la définition des fonctions analytiques d’une ou de plusieurs variables complexes, qui est une branche fondamentale de l’analyse ^{[cf. FONCTIONS ANALYTIQUES]}. Soit (z ⁿ ) une suite de nombres complexes et soit (s ⁿ ) la suite des sommes partielles:

on dit que la série de terme général z ⁿ , ou que la série: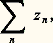

est convergente de somme S, et on écrit:

si la suite (s ⁿ ) converge vers S. Les séries permettent de définir de nombreuses fonctions; ainsi, la série de terme général z ⁿ /n ! converge pour tout nombre complexe z et sa somme, la fonction exponentielle complexe:

est sans conteste une des fonctions les plus importantes des mathématiques ^{[cf. EXPONENTIELLE ET LOGARITHME]}. La règle de multiplication des séries permet d’établir la propriété fondamentale de la fonction exponentielle: si z et z sont deux nombres complexes, on a:

3. Forme trigonométrique

Trigonométrie

Les nombres complexes de module 1 peuvent être caractérisés comme les nombres complexes 0 dont le conjugué et l’inverse sont égaux; on vérifie facilement qu’ils forment un groupe multiplicatif que nous désignerons par U. Les images des éléments de U sont les points du cercle de centre O et de rayon 1 (appelé souvent «cercle trigonométrique»); l’application qui au nombre complexe u 捻 U, d’image M, fait correspondre l’angle A(u ) du demi-axe réel positif avec la demi-droite OM est un isomorphisme du groupe multiplicatif U sur le groupe additif des angles orientés de demi-droites et pourrait d’ailleurs servir à donner une définition rigoureuse de ces angles. L’étude du groupe U constitue ce qu’on appelle traditionnellement la trigonométrie; l’outil pour définir de façon correcte les fonctions trigonométriques est la fonction exponentielle complexe.

Pour tout nombre réel t , le nombre complexe e ^it appartient à U. En effet, on voit facilement sur le développement en série de e ^z que le conjugué de e ^z est e ^z pour tout nombre complexe z ; on a donc, en utilisant aussi (),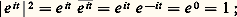

la formule () montre aussi que l’on a:

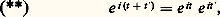ce qui exprime que l’application qui au nombre réel t associe le nombre complexe e ^it 捻 U est un homomorphisme du groupe additif R sur le groupe multiplicatif U.

Par définition, on appelle cos t et sin t respectivement les parties réelle et imaginaire de e ^it , soit:

puisque |e ^it | = 1, on a cos²t + sin²t = 1 pour tout nombre réel t .

L’étude de e ^{it [cf. EXPONENTIELLE ET LOGARITHME]} montre alors qu’il existe un nombre réel 神 礪 0 tel que e ⁱ size=1^{神/ 2} = i et tel que l’application qui à t associe e ^it soit une bijection de l’intervalle [0, 2 神[ sur U. Puisque, d’après ():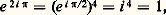

on en déduit, toujours d’après (), que la fonction e ^it est périodique de période 2 神. Ainsi, tout nombre complexe u de module 1 s’écrit sous la forme:

où t est un nombre réel déterminé à 2 k 神 près, k entier relatif; cela revient à dire que si x et y sont deux nombres réels tels que x ² + y ² = 1, il existe un nombre réel t , défini à 2 k 神 près, tel que x = cos t et y = sin t . La propriété () montre, d’autre part, que si t et t sont deux nombres réels, on a: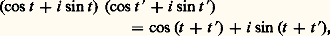

ce qui, en égalant les parties réelles et imaginaires des deux membres, donne les formules trigonométriques d’addition des arguments. On déduit facilement de ce qui précède la formule de De Moivre, valable pour tout entier relatif n ,

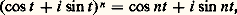qui permet d’obtenir de nombreuses formules de trigonométrie.

Forme trigonométrique

Nous désignerons par C le groupe multiplicatif des nombres complexes non nuls. Si z 0, le nombre complexe z / |z | est de module 1 et on voit facilement que l’application qui à tout nombre complexe z 0 associe le couple (|z |, z /|z |) est une bijection de C sur l’ensemble R⁺ 憐 U des couples (r , u ) d’un nombre réel r 礪 0 et d’un élément u 捻 U; la bijection réciproque associe à un tel couple (r , u ) le nombre complexe ru , de module r . L’étude de U faite ci-dessus permet donc d’écrire tout nombre complexe z 0 sous la forme:

appelée forme trigonométrique du nombre complexe z. On dit qu’une telle valeur de t est un argument de z ; quand on connaît une valeur de l’argument, on obtient donc toutes les autres en lui ajoutant un multiple entier relatif de 2 神 et deux nombres complexes sont égaux si et seulement s’ils ont le même module et des arguments qui diffèrent de 2 k 神, k entier relatif. Si on impose à l’argument d’appartenir à l’intervalle ] 漣 神, + 神], il est déterminé de manière unique et s’appelle l’argument principal .

Racines n-ièmes

La recherche des nombres complexes z tels que z ⁿ = 1 va montrer l’intérêt de la forme trigonométrique. Écrivant z sous forme trigonométrique: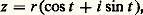

on doit avoir:

les nombres z ⁿ et 1 sont égaux s’ils ont le même module, soit r ⁿ = 1, d’où r = 1, et s’ils ont des arguments qui diffèrent d’un multiple entier de 2 神, soit nt = 2 k 神, avec k entier relatif, en prenant 0 pour argument de 1. On peut donc écrire t = 2 k 神/n ; si on se limite aux valeurs de t appartenant à l’intervalle [0, 2 神], il suffit de donner à k les n valeurs successives 0, 1, 2, ..., n 漣1, car toute autre valeur de k donne des valeurs correspondantes de t égales, à un multiple de 2 神 près, aux valeurs de t obtenues pour ces nombres. On obtient ainsi n nombres complexes de module 1 distincts: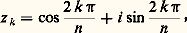

où k = 0, 1, 2, ..., n 漣 1; ces nombres complexes sont les n racines du polynôme z ⁿ 漣 1 et leurs images sont les sommets d’un polygone régulier inscrit dans le cercle trigonométrique (fig. 2).

Un raisonnement analogue montrerait que tout nombre complexe non nul a n racines n -ièmes distinctes; si c est l’une d’entre elles, ces racines sont: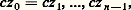

où les z ^k sont les racines n -ièmes de 1.

Encyclopédie Universelle. 2012.